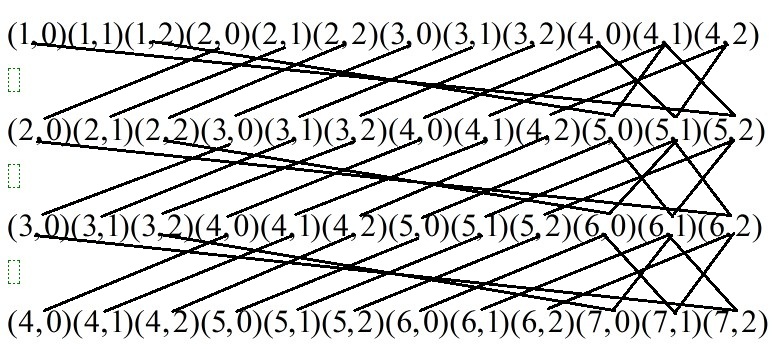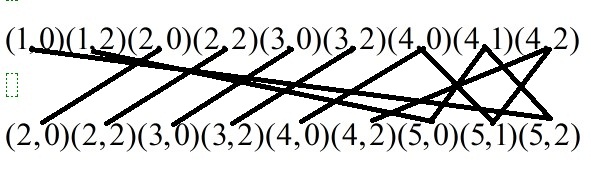题目链接:
题意:一个n进制(2<=n<=6)的数字,满足以下条件:(1)至少包含两位且不以0开头,比如012是不行的;(2)相邻数字不同;(3)定义这个数字x的score(x)等于相邻数字差的平方和,比如score(125)=(1-2)*(1-2)+(2-5)*(2-5)=10。现在给出n和m,求满足条件的所有n进制的数字中有多少数字的score为m。(1<=m<=10^9)
思路:首先我们使用简单的DP,设f[i][j]表示和为i以j结尾的数字个数。由于这个m很大,这样肯定是不行的。我们发现,这个DP转移的时候每次都是一样的,这正是可以运用矩阵的地方。我们将条件(1)中不能以0开头改为不能以0结尾,这其实是等价的。以下以n=3为例。我们用(i,j)表示和为i以j结尾的方案数,使用矩阵递推时,设矩阵为a,用s[m]表示score为m的方案数,我们用[s[1],s[2],s[3],s[4]]*a=[s[2],s[3],s[4],s[5]],因为要加上以j结尾的状态,我们用s[i,j]表示以j结尾score为i为方案数,简写为(i,j)。那么我们给出完整的递推:
我们说明一下,比如第一行向第二行递推的时候,(1,1)可以向(2,2)递推的为什么我们不连呢?因为我们在第一行计算(2,2)时,就已经计算了从(1,1)转移过来的情况了。所以第一行除了向(5,0)(5,1)(5,2)连边外,其他的直接连下来。现在,有木有发现第一行有三个状态自始至终都没有用到,(1,1)(2,1)(3,1),为什么?其实我们以后能够到的只是可以递推到大于等于5的,而最有可能的(3,1)也只能递推到4,即后面加一个0或者2,所以我们可以将这些冗余状态删除。完了,就成这样了:
这样当n=6时,也只有100个状态,而不是开始的6*5*5=150个状态。比如计算n=6,m=1000,只有计算出a=a^(m-25)(a为转移矩阵),然后用S[i,j]这个数组,就是从S[1,0]到S[4,2]共9个元素,分别乘以a的最后(n-1)列?为什么不是n列呢?因为我们上面说转换为以0结尾,所以最后不能以0结尾。
#include <iostream>
#include <cstdio>#include <string.h>#include <algorithm>#include <cmath>#include <vector>#include <queue>#include <set>#include <stack>#include <string>#include <map>#define max(x,y) ((x)>(y)?(x):(y))#define min(x,y) ((x)<(y)?(x):(y))#define abs(x) ((x)>=0?(x):-(x))#define i64 long long#define u32 unsigned int#define u64 unsigned long long#define clr(x,y) memset(x,y,sizeof(x))#define CLR(x) x.clear()#define ph(x) push(x)#define pb(x) push_back(x)#define Len(x) x.length()#define SZ(x) x.size()#define PI acos(-1.0)#define sqr(x) ((x)*(x))#define MP(x,y) make_pair(x,y)#define FOR0(i,x) for(i=0;i<x;i++)#define FOR1(i,x) for(i=1;i<=x;i++)#define FOR(i,a,b) for(i=a;i<=b;i++)#define rush() int CC;for(scanf("%d",&CC);CC--;)#define Rush(n) while(scanf("%d",&n)!=-1)using namespace std;void RD(int &x){scanf("%d",&x);}void RD(i64 &x){scanf("%I64d",&x);}void RD(u32 &x){scanf("%u",&x);}void RD(double &x){scanf("%lf",&x);}void RD(int &x,int &y){scanf("%d%d",&x,&y);}void RD(i64 &x,i64 &y){scanf("%I64d%I64d",&x,&y);}void RD(u32 &x,u32 &y){scanf("%u%u",&x,&y);}void RD(double &x,double &y){scanf("%lf%lf",&x,&y);}void RD(int &x,int &y,int &z){scanf("%d%d%d",&x,&y,&z);}void RD(i64 &x,i64 &y,i64 &z){scanf("%I64d%I64d%I64d",&x,&y,&z);}void RD(u32 &x,u32 &y,u32 &z){scanf("%u%u%u",&x,&y,&z);}void RD(double &x,double &y,double &z){scanf("%lf%lf%lf",&x,&y,&z);}void RD(char &x){x=getchar();}void RD(char *s){scanf("%s",s);}void RD(string &s){cin>>s;}void PR(int x) {printf("%d\n",x);}void PR(int x,int y) {printf("%d %d\n",x,y);}void PR(i64 x) {printf("%I64d\n",x);}void PR(u32 x) {printf("%u\n",x);}void PR(double x) {printf("%.3lf\n",x);}void PR(char x) {printf("%c\n",x);}void PR(char *x) {printf("%s\n",x);}void PR(string x) {cout<<x<<endl;}const i64 inf=((i64)1)<<60;const double dinf=1e50;const int INF=1000000000;const int N=1005;int M;class Matrix{ public: u32 a[160][160]; void init(int x) { int i,j; FOR0(i,M) FOR0(j,M) a[i][j]=0; if(x==1) { FOR0(i,M) a[i][i]=1; } } Matrix operator*(Matrix p) { Matrix ans; ans.init(0); int i,j,k; FOR0(k,M) FOR0(i,M) FOR0(j,M) { ans.a[i][j]+=a[i][k]*p.a[k][j]; } return ans; } Matrix Pow(int n) { Matrix ans,p=*this; ans.init(1); while(n) { if(n&1) ans=ans*p; p=p*p; n>>=1; } return ans; } void print() { puts(""); int i,j; FOR0(i,M) { FOR0(j,M) printf("%u ",a[i][j]); puts(""); } puts(""); }};Matrix a;int n,m;int f[26][6],b[26][6],c[120];int DFS(int sum,int pre){ if(sum==0) return 1; if(sum<0) return 0; if(f[sum][pre]!=-1) return f[sum][pre]; int ans=0,i; FOR0(i,n) if(i!=pre) ans+=DFS(sum-sqr(i-pre),i); return f[sum][pre]=ans;}int OK(int i,int j){ int k; FOR0(k,n) if(k!=j&&i+sqr(j-k)>=(n-1)*(n-1)+1) return 1; return 0;}void initMatrix(){ clr(f,-1); clr(b,0); int i,j,k,X=(n-1)*(n-1); M=0; FOR1(i,X) FOR0(j,n) if(OK(i,j)) { c[M]=DFS(i,j); b[i][j]=M++; } a.init(0); int x,y; FOR0(i,n) FOR0(j,n) if(i!=j) { x=b[X+1-sqr(i-j)][j]; y=b[X][i]; a.a[x][y]++; } for(i=2;i<=X;i++) FOR0(j,n) if(OK(i-1,j)) { x=b[i][j]; y=b[i-1][j]; a.a[x][y]++; }}int main(){ int num=0; rush() { RD(n,m); printf("Case %d: ",++num); if(n==2) { puts("1"); continue; } initMatrix(); u32 ans=0; int i,j; if(m<=(n-1)*(n-1)) { FOR1(i,n-1) ans+=DFS(m,i); PR(ans); continue; } a=a.Pow(m-(n-1)*(n-1)); FOR0(i,M) for(j=M-n+1;j<M;j++) ans+=c[i]*a.a[i][j]; PR(ans); }}